Monotonieverhalten
Als Monotonieverhalten bezeichnet man das Steigungsverhalten einer Funktion. Dieses gibt Auskunft darüber, wann eine Funktion steigt oder fällt.
Allgemein
- monoton steigend, wenn $f(x_1)\le f(x_2)$
- monoton fallend, wenn $f(x_1)\ge f(x_2)$
- streng monoton steigend, wenn $f(x_1)< f(x_2)$
- streng monoton fallend, wenn $f(x_1)> f(x_2)$
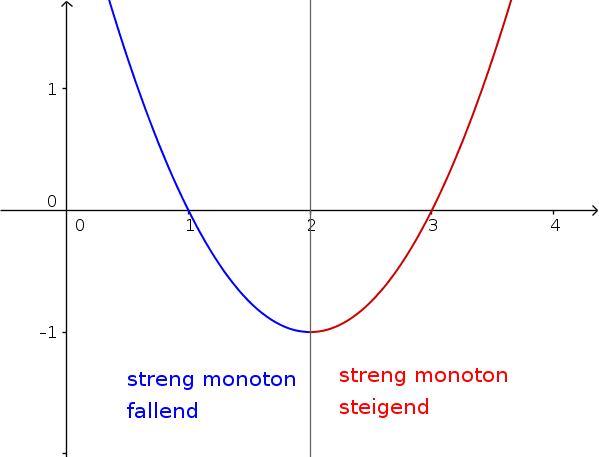
Merke
Die Funktion ist auf dem Intervall $I$ differenzierbar und
- monoton steigend, wenn für alle $x\in I$ gilt $f'(x)\ge0$
- monoton fallend, wenn für alle $x\in I$ gilt $f'(x)\le0$
- streng monoton steigend, wenn für alle $x\in I$ gilt $f'(x)>0$
- streng monoton fallend, wenn für alle $x\in I$ gilt $f'(x)<0$
Vorgehensweise
- Ableitung bestimmen
- Nullstelle(n) der Ableitung berechnen
- Intervalle bestimmen
- Probeeinsetzung in die Ableitung
Beispiel
Untersuche die Funktion $f(x)=x^3+2x^2-4x-8$ auf Monotonie.
-
Ableitung bestimmen
$f'(x)=3x^2+4x-4$ -
Nullstellen der Ableitung berechnen
Es liegt eine quadratische Gleichung vor, die man beispielsweise mit der PQ-Formel lösen kann.
$f'(x)=3x^2+4x-4\quad|:3$
$f'(x)=x^2+\frac43x-\frac43$
$x_{1,2} = -\frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
$x_{1,2} = -\frac{2}{3} \pm\sqrt{(\frac23)^2+\frac43}$
$x_{1,2} = -\frac{2}{3} \pm\sqrt{\frac{16}{9}}$
$x_{1,2} = -\frac{2}{3} \pm\frac43$
$x_1=\color{blue}{-2} \quad x_2=\color{green}{\frac23}$ -
Intervalle bestimmen
Mit den Nullstellen der Ableitungsfunktion bildet man nun die Intervalle, bei denen man das Monotonieverhalten untersucht.
$x_1=\color{blue}{-2} \quad x_2=\color{green}{\frac23}$
$I_1(-\infty|\color{blue}{-2})$, $I_2(\color{blue}{-2}|\color{green}{\frac23})$, $I_3(\color{green}{\frac23}|\infty)$ -
Probeeinsetzungen in die Ableitung
Jeweils einen beliebigen Wert aus jedem Intervall in die Ableitung einsetzen.
$I_1(-\infty|-2)$:
Probeeinsetzung: $x=\color{red}{-3}$
$f'(\color{red}{-3})=3\cdot(\color{red}{-3})^2+4\cdot(\color{red}{-3})-4$ $=11 > 0$
=> Die Ableitung ist im Intervall $I_1$ positiv, d.h. die Funktion ist in diesem Intervall monoton steigend.
$I_2(-2|\frac23)$:
Probeeinsetzung: $x=\color{red}{0}$
$f'(\color{red}{0})=3\cdot\color{red}{0}^2+4\cdot\color{red}{0}-4$ $=-4 < 0$
=> Die Ableitung ist im Intervall $I_2$ negativ, d.h. die Funktion ist in diesem Intervall monoton fallend.
$I_3(\frac23|\infty)$:
Probeeinsetzung: $x=\color{red}{1}$
$f'(\color{red}{1})=3\cdot\color{red}{1}^2+4\cdot\color{red}{1}-4$ $=3 > 0$
=> Die Ableitung ist im Intervall $I_3$ positiv, d.h. die Funktion ist in diesem Intervall monoton steigend.
Monotonieverhalten Teil 1: Erklärung, Begriffe: (streng) monoton steigend / (streng) monoton fallend
Da es sich beim Monotonieverhalten um das Steigungsverhalten handelt, betrachtet man zur Bestimmung die Ableitung, da diese die Steigung der Funktion in Abhängigkeit von $x$ angibt.
- eine positive Ableitung (Steigung) entspricht monoton steigend
- eine negative Ableitung (Steigung) entspricht monoton fallend
Strenge Monotonie bezeichnet den Fall, dass die Steigung bzw. Ableitung im Intervall nie bei 0 liegt.
Monotonieverhalten Teil 2: Monotonieverhalten rechnerisch bestimmen, erste Ableitung
Um die möglichen Stellen für einen Vorzeichenwechsel der Ableitung $f'$ zu bestimmen, berechnet man die Nullstellen von $f'$. Nur an diesen Stellen kann sich das Monotonieverhalten der Ausgangsfunktion $f$ ändern. Anschließend nutzt man einen beliebigen Wert pro enstandenem Intervall den man in die Ableitung einsetzt, um zu entscheiden, ob der Funktionsgraph in diesem Intervall steigt oder fällt.