Bestimmte Integrale

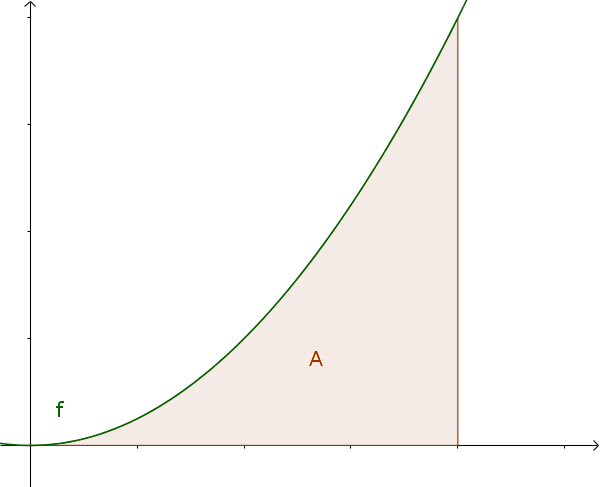
Die Integralrechnung wird zur Berechnung der Fläche in einem Intervall zwischen dem Graphen einer Funktion und der x-Achse genutzt.

$Fläche unter einem Funktionsgraphen$

Info

Die Fläche unterhalb eines Graphen kann mit der Streifenmethode hergeleitet werden. Dazu bildet man den Grenzwert der Ober- und Untersummen mit der Streifenzahl $n$ für $n\to\infty$. Es gilt:

$\text{Untersumme} \le A \le \text{Obersumme}$

Diese Fläche wird durch das bestimmte Integral abgebildet. Es hängt ausschließlich von der Funktion und den Integrationsgrenzen $a$ und $b$ ab.

$\int_a^b f(x)\,\mathrm{d}x$

Berechnung bestimmter Integrale

Das Ergebnis eines bestimmten Integrals ist immer eine eindeutige, feste Zahl und kann mit dem Hauptsatz der Differenzial- und Integralrechnung berechnet werden.

$\int_a^b f(x) \, \mathrm{d}x = F(b) - F(a)$

Hauptsatz der Differenzial- und Integralrechnung

Der Hauptsatz der Differenzial- und Integralrechnung ist von zentraler Bedeutung in der Infinitesimalrechnung. Er

wird benutzt bei der Berechnung bestimmter Integrale.
verbindet das bestimmte mit dem unbestimmten Integral.
stellt den Zusammenhang zwischen Differenzial- und Integralrechnung dar.

Berechnung

Entscheidend für die Berechnung ist die Stammfunktion $F$, die den summierten Flächeinhalt bis zu einer Stelle $x$ unterhalb der Funktion angibt. Beim bestimmten Integral wird allerdings nur der Flächeinhalt im Integrationsintervall $[a; b]$ gesucht. Also wird vom gesamten Flächeninhalt bis zu Stelle b, nämlich $F(b)$, noch der Teil $F(a)$ abgezogen.

Häufig wird in eckigen Klammern die Stammfunktion $F$ als Zwischenschritt notiert. Die Stammfunktion erhält man durch das Integrieren bzw. Berechnen des unbestimmten Integrals. Beachte beim bestimmten Integral immer weiterhin die Integrationsgrenzen anzugeben.

$\int_a^b f(x) \, \mathrm{d}x = [F(x) + C]_a^b = F(b) - F(a)$

Rechenregeln

Gleiche untere und obere Grenze
$\int_a^a f(x) \, \mathrm{d}x=0$
Vertauschung der Grenzen
$\int_a^b f(x) \, \mathrm{d}x$ $=-\int_b^a f(x) \, \mathrm{d}x$
Intervalladditivität
$\int_a^b f(x) \, \mathrm{d}x + \int_b^c f(x) \, \mathrm{d}x$ $=\int_a^c f(x) \, \mathrm{d}x$
Faktorregel
$\int_a^b k\cdot f(x) \, \mathrm{d}x$ $= k\cdot \int_a^b f(x) \, \mathrm{d}x$
Summenregel
$\int_a^b (f(x)+g(x)) \, \mathrm{d}x$ $= \int_a^b f(x) \, \mathrm{d}x + \int_a^b g(x) \, \mathrm{d}x$