Angles between two vectors
Using the scalar product you can determine the angle between two vectors.
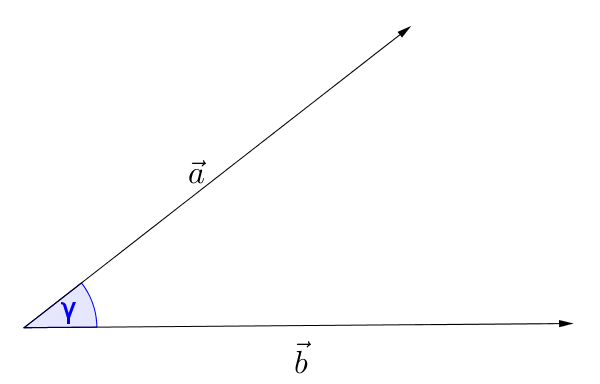
The following formula is used to calculate:
$\cos(\gamma) = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}$
$\gamma = \cos^{-1}\left(\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\right)$
$\gamma = \cos^{-1}\left(\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\right)$
Example
Determine the angle between $\vec{a}=\begin{pmatrix}2\\6\\-3\end{pmatrix}$ and $\vec{b}=\begin{pmatrix}2\\3\\5\end{pmatrix}$.
Calculate the scalar product
$\vec{a}\cdot\vec{b}$ $=\begin{pmatrix}2\\6\\-3\end{pmatrix}\cdot\begin{pmatrix}2\\3\\5\end{pmatrix}$ $=2\cdot2+6\cdot3-3\cdot5$ $=7$Calculate the vector length
$|\vec{a}|=\sqrt{2^2+6^2+(-3)^2}$ $=7$
$|\vec{b}|=\sqrt{2^2+3^2+5^2}$ $=\sqrt{38}$Insert results in the formula
$\cos(\gamma) = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}$
$\cos(\gamma) = \frac{7}{7\cdot\sqrt{38}}$ $= \frac{1}{\sqrt{38}}$
$\gamma = \cos^{-1}\left(\frac{1}{\sqrt{38}}\right)$ $\approx80.66°$