Mathe ↠ Ableitung anwenden

Ableitung anwenden

Der Begriff der Ableitung oder Ableitungsfunktion $f'$ sollte bereits bekannt sein. Sie gibt die Steigung der Tangenten von der Funktion $f$ an der Stelle $x$ an.

Steigung und Tangente

Als Tangente bezeichnet man eine Gerade, die an genau einem Punkt des Graphen anliegt und ihre Steigung dem Differenzialquotienten entspricht.

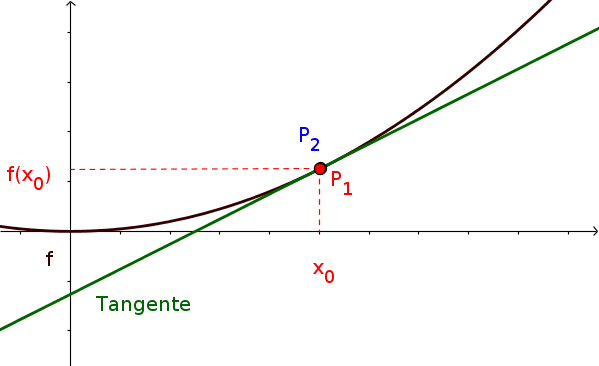
Tangente an einem Punkt

Bei der Tangenten handelt es sich um den Graphen einer linearen Funktion. Die Funktionsgleichung besteht also aus einer Steigung $m$ und dem y-Achsenabschnitt $n$:

$t(x)=mx+n$

Meistens hat man einen Punkt $P(x|y)$ und eine Funktion $f$ gegeben und soll die Tangentengleichung aufstellen. Die Steigung wird durch Einsetzen von $x$ in die Ableitung $f'$ berechnet. Anschließend wird der y-Achsenabschnitt bestimmt, indem man den Punkt $P$ in die Gleichung einsetzt und nach $n$ auflöst.

!

Merke

Zum Berechnen der Steigung der Tangenten wird die Stelle $x$ in die Ableitung eingesetzt: $m=f'(x)$

Steigungswinkel und Schnittwinkel

Der Steigungswinkel $\alpha$ einer Funktion $f$ an der Stelle $x$ lässt sich mit der Ableitung $\color{green}{f'}$ berechnen:

$\alpha=\arctan(\color{green}{f'(x)})$

Es handelt sich um den Steigungswinkel der Tangenten an dieser Stelle. Zu Berechnung wird nur die Steigung benötigt und in den Arkustangens eingesetzt.

Steigungswinkel mit Tangente bestimmen

Schnittwinkel

Wenn sich die Graphen von zwei Funktionen schneiden, bilden die Tangenten zwei Winkel miteinander. Der kleinere Winkel wird als Schnittwinkel $\gamma$ bezeichnet.

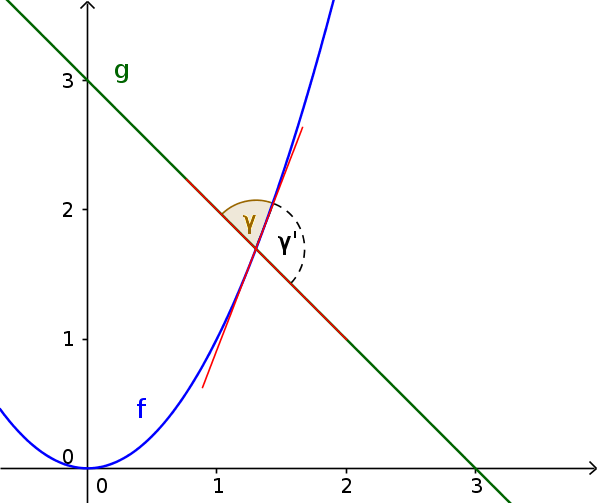
Schnittwinkel von Funktionen

Zur Berechnung benötigt man den Schnittpunkt sowie die Steigungswinkel der Funktionen $\alpha$ und $\beta$ am Schnittpunkt. Diese werden in die folgenden Formeln eingesetzt und der kleinere Wert entspricht dem Schnittwinkel.

$\gamma_1=|\alpha-\beta|$ bzw. $\gamma_2=180^\circ-|\alpha-\beta|$

Berührpunkte

Ein Berührpunkt ist eine besondere Art von Schnittpunkt, da dort nicht nur die Funktionswerte sondern auch die Steigungen übereinstimmen.

!

Merke

Zwei Funktionen besitzen einen Berührpunkt, wenn gilt:
$f(x_B)=g(x_B)$ und
$f'(x_B)=g'(x_B)$

Das Vorgehen zum Bestimmen von Berührpunkten:

  1. Ableitungen der Funktionen bilden
  2. Schnittpunkte berechnen: Funktionsgleichungen gleichsetzen: $f(x_B)=g(x_B)$
  3. Steigungen überprüfen: Kriterium $f'(x_B)=g'(x_B)$ erfüllt?
  4. Berührpunkt angeben
Quiz über Ableitung anwenden starten