Quadratische Funktionen
Eine quadratische Funktion ist jede Funktion mit der allgemeinen Gleichung:
$f(x)=ax^2+bx+c$
Graph einer quadratischen Funktion
Den Graphen einer quadratischen Funktion bezeichnet man als Parabel.
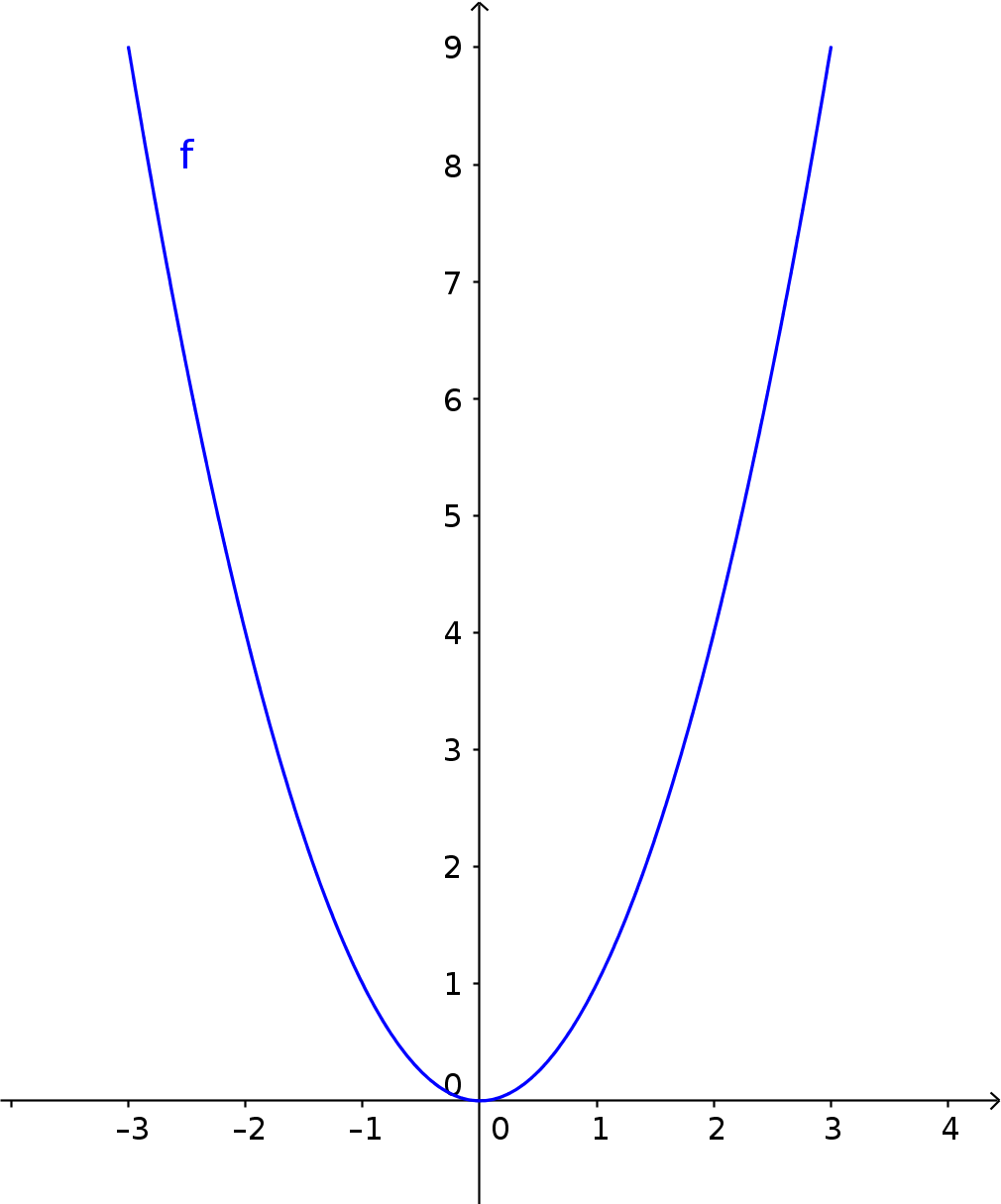
In der Abbildung handelt es sich um die einfachste quadratische Funktion mit der Funktionsgleichung $f(x)=x^2$. Ihr Graph ist die sogenannte Normalparabel.
Strecken und Stauchen
Die Normalparabel lässt sich mit dem Parameter $a$ strecken und stauchen.
$f(x)=ax^2$
!
Merke
- Wenn $|a|$ > 1, ist der Graph steiler als die Normalparabel und wird gestreckt.
- Wenn $|a|$ < 1, ist der Graph flacher als die Normalparabel und wird gestaucht.
Spiegeln der Normalparabel
Die Normalparabel lässt sich mit einem negativen Parameter $a$ auch spiegeln.
Beispiel
$\color{blue}{f(x)=x^2}$
$\color{green}{g(x)=-x^2}$
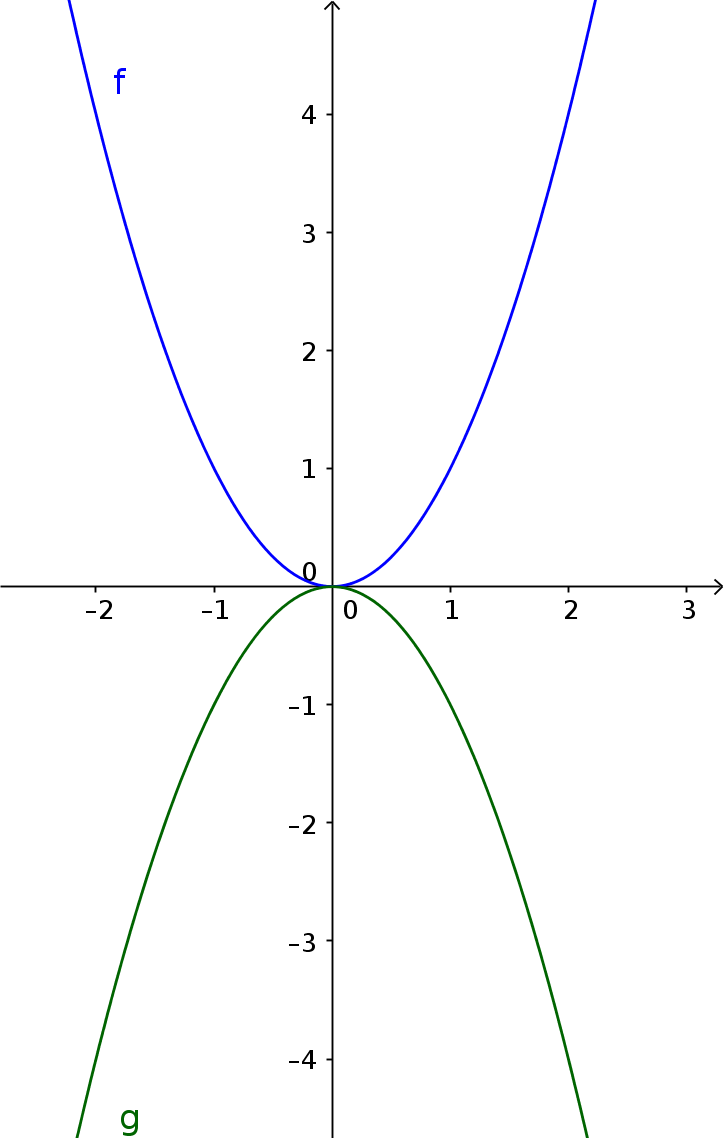
Verschieben der Normalparabel
Je nach Funktionsgleichung kann man eine Parabel auch in x- oder y-Richtung verschieben
Entlang der y-Achse
$f(x)=x^2+c$
Mit dem Paramter $c$ kann die Normalparabel in y-Richtung, also nach oben und unten, verschoben werden.
!
Merke
- Wenn $c$ > 0, wird der Graph nach oben verschoben.
- Wenn $c$ < 0, wird der Graph nach unten verschoben.
Entlang der x-Achse
$y=(x+d)^2$
Die Normalparabel lässt sich mit dem Parameter $d$ in x-Richtung verschieben.
!
Merke
- Wenn $d$ < 0, wird der Graph nach rechts verschoben.
- Wenn $d$ > 0, wird der Graph nach links verschoben.
Scheitelpunktform
Durch die Möglichkeiten des Verschiebens und Streckens erhält man folgende sogenannte Scheitelpunktform, aus der sich der Scheitelpunkt $S(\color{blue}{d}|\color{green}{c})$ der Parabel direkt ablesen lässt. Als Scheitelpunkt bezeichnet man den höchsten (bei nach unten geöffneter Parabel) bzw. tiefsten Punkt (bei nach oben geöffneter Parabel) der Funktion.
$f(x)=a(x-\color{blue}{d})^2+\color{green}{c}$
Um aus der allgemeinen Form $f(x)=ax^2+bx+c$ in die Scheitelpunktform zu kommen, nutzt man die quadratische Ergänzung.
Lernen
Üben
Premium-
Grundlagen
3 AufgabenFunktionsgraphen zeichnen und ablesen
4 AufgabenNullstellenberechnung
3 AufgabenSchnittpunktberechnung
3 Aufgaben
